논리와비판적사고 문제 풀어주세요 문제 풀어주세요....
좋은 문제네요. 정언삼단논법을 **현대적 관점(벤 다이어그램)**에서 타당성만 따져보겠습니다.
핵심은 결론이 전제로부터 논리적으로 필연적으로 나오는가입니다. (내용의 사실 여부 X)
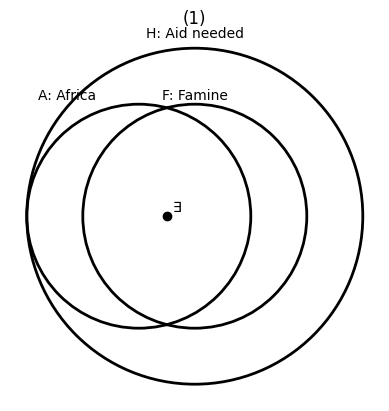
(1) 아프리카 국가 – 해외원조 논증
문장 구조 정리
결론:
어떤 아프리카 국가는 해외원조가 필요한 국가이다
전제 1:
어떤 아프리카 국가는 국민들이 기아로 죽어간다
전제 2:
국민들이 기아로 죽어가는 모든 국가는 해외원조가 필요하다
범주로 정리 (벤 다이어그램용)
A: 아프리카 국가
H: 해외원조가 필요한 국가
F: 국민들이 기아로 죽어가는 국가
전제들을 기호로 쓰면:
∃(A ∧ F)
∀(F → H)
결론: ∃(A ∧ H)
논리 판단
전제1에서 A ∩ F에 실제로 어떤 대상이 존재
전제2에 의해 F ⊆ H
따라서 A ∩ H에도 반드시 어떤 대상이 존재
결론이 필연적으로 따라옵니다
✅ 논리적으로 타당 (Valid)
※ 감정적·정치적 표현과 무관하게 형식만 보면 완벽히 타당
(2) 테러리스트 – 비행기 폭파범 논증
문장 구조 정리
전제 1:
인간의 생명을 중시하는 모든 사람은 테러리스트가 아니다
전제 2:
모든 비행기 폭파범은 테러리스트이다
결론:
모든 비행기 폭파범은 인간의 생명을 중시하는 사람이 아니다
범주 설정
L: 인간의 생명을 중시하는 사람
T: 테러리스트
B: 비행기 폭파범
기호로 쓰면:
∀(L → ¬T)
(대우: ∀(T → ¬L))
∀(B → T)
결론: ∀(B → ¬L)
논리 연결
전제2: B ⊆ T
전제1의 대우: T ⊆ ¬L
따라서 B ⊆ ¬L
전제들을 연결하면 결론이 자동으로 도출
✅ 논리적으로 타당 (Valid)
최종 정리
| 문항 | 타당성 | 이유 |
| (1) | ✅ 타당 | 존재명제 + 포함관계가 결론 보장 |
| (2) | ✅ 타당 | 포함관계의 연쇄 + 대우 성립 |
벤 다이어그램 직접 그려서 설명
----------------------
**전통 정언 삼단논법(S·P·M)**으로 형식만 깔끔하게 정리합니다.
(감정·내용 판단 ❌ / 논리형식 ⭕ / 시험용)
(1) 아프리카 국가 – 해외원조 논증
용어 지정
S (소항): 아프리카 국가
P (대항): 해외원조가 필요한 국가
M (중항): 국민들이 기아로 죽어가는 국가
전통 삼단논법 형식
대전제
모든 M는 P이다.
(기아 국가는 모두 해외원조가 필요하다)
소전제
어떤 S는 M이다.
(어떤 아프리카 국가는 기아 상태이다)
결론
어떤 S는 P이다.
(어떤 아프리카 국가는 해외원조가 필요하다)
형식 판정
형식: Darii
도형(Figure): 1형식
표준 정언삼단논법
✅ 타당 (Valid)
(2) 테러리스트 – 비행기 폭파범 논증
용어 지정
S (소항): 비행기 폭파범
P (대항): 인간의 생명을 중시하는 사람
M (중항): 테러리스트
전통 삼단논법 형식
대전제
모든 P는 M이 아니다.
(생명을 중시하는 사람은 테러리스트가 아니다)
소전제
모든 S는 M이다.
(비행기 폭파범은 모두 테러리스트다)
결론
어떤 S도 P가 아니다.
(어떤 비행기 폭파범도 생명을 중시하지 않는다)
※ 정언형으로 쓰면
모든 S는 비(非)P이다
형식 판정
형식: Celarent 변형 (부정항 포함)
도형(Figure): 1형식
대우·부정 처리 후 정형 삼단논법
✅ 타당 (Valid)
시험에서 바로 쓰는 체크 포인트
| 항목 | (1) | (2) |
| 중항 분배 | ⭕ | ⭕ |
| 부정 전제 | ❌ | ⭕ (1개) |
| 결론 부정 | ❌ | ⭕ |
| 존재 가정 | ⭕ | ❌ |
| 타당성 | ✅ | ✅ |
한 줄 요약 (서술형 답안용)
(1)은 Darii형의 정언삼단논법으로 타당하며,
(2)는 부정 전제를 포함한 1형식 삼단논법으로 결론이 필연적으로 도출되므로 타 당하다.